Math Topics Before Square Root Grade Level: Building a Strong Foundation

Understanding when and how mathematical concepts build upon each other helps parents and educators support student learning effectively. Before students encounter square roots, they need a solid foundation in several key mathematical areas. Study Watches provides comprehensive educational resources to help track student progress through these important mathematical milestones.
The journey toward understanding advanced mathematical concepts requires careful scaffolding of skills. Each mathematical topic serves as a building block for more complex ideas that students will encounter later in their academic careers.
Most educators introduce square roots around eighth or ninth grade, but what grade is square root taught can vary depending on the curriculum and individual student readiness. Before reaching this milestone, students must master several foundational concepts that prepare them for success.
Essential Number Sense and Basic Operations
Students need strong number sense before approaching square roots. This includes understanding place value, number relationships, and basic computational skills. Children typically develop these skills throughout elementary school.
Basic arithmetic operations form the cornerstone of mathematical understanding. Students must demonstrate fluency in addition, subtraction, multiplication, and division before moving to more complex topics. These operations should become automatic rather than requiring extensive mental calculation.
Understanding factors and multiples becomes crucial for later square root work. Students learn that some numbers can be broken down into smaller parts through factorization. This concept appears frequently in middle school mathematics curricula.
Fraction and Decimal Mastery
Working with fractions requires students to understand parts of wholes and equivalent relationships. This understanding directly connects to square root concepts, especially when dealing with irrational numbers and decimal approximations.
Converting between fractions, decimals, and percentages gives students flexibility in mathematical thinking. These conversions help students recognize that numbers can be expressed in multiple forms while maintaining the same value.
Operations with fractions and decimals must be solid before introducing square roots. Students should confidently add, subtract, multiply, and divide these number types without relying heavily on calculators.
Introduction to Exponents and Powers
Understanding exponents provides the foundation for square root comprehension. Students learn that exponents represent repeated multiplication, such as 3² meaning 3 × 3.
Perfect squares emerge naturally from exponent work. When students calculate 4², 5², and 6², they begin recognizing patterns that will later connect to square root concepts.
The relationship between squaring numbers and finding square roots becomes clearer when students have solid exponent understanding. This reciprocal relationship helps students grasp why square roots exist as mathematical operations.
Geometry Foundations
Basic geometric concepts support square root learning through practical applications. Students encounter area calculations for squares and rectangles, which naturally lead to questions about side lengths when given areas.
The Pythagorean theorem introduces students to square roots in a concrete context. Finding the length of a triangle’s hypotenuse requires square root calculations, making the concept meaningful rather than abstract.
Coordinate geometry provides another avenue for square root applications. Calculating distances between points on a coordinate plane requires students to use square roots in the distance formula.
Order of Operations and Algebraic Thinking
Students must understand order of operations before tackling complex expressions involving square roots. The acronym PEMDAS helps students remember the correct sequence for mathematical operations.
Basic algebraic thinking develops through pattern recognition and simple equation solving. Students learn to work with variables and understand that letters can represent unknown quantities.
Solving simple equations prepares students for more complex algebraic manipulation involving square roots. Understanding inverse operations becomes particularly important for this advanced work.
Problem-Solving Strategies
Mathematical reasoning skills develop gradually through exposure to various problem types. Students learn to break down complex problems into manageable steps.
Estimation skills help students check the reasonableness of their square root calculations. Understanding that the square root of 50 falls between 7 and 8 requires solid number sense.
Multiple solution strategies give students flexibility in approaching square root problems. Some students prefer factoring methods, while others work better with decimal approximations.
Technology Integration
Calculator skills become important as students approach square root topics. Understanding when and how to use technology appropriately supports learning rather than replacing mathematical thinking.
Graphing concepts introduce students to visual representations of mathematical relationships. Seeing how y = x² relates to finding square roots helps students understand inverse functions.
Digital tools can provide interactive experiences with square root concepts. Many educational platforms offer visual demonstrations that make abstract concepts more concrete.
Assessment and Readiness Indicators
Teachers look for specific indicators when determining student readiness for square root instruction. Fluency with multiplication tables through 12 × 12 provides essential background knowledge.
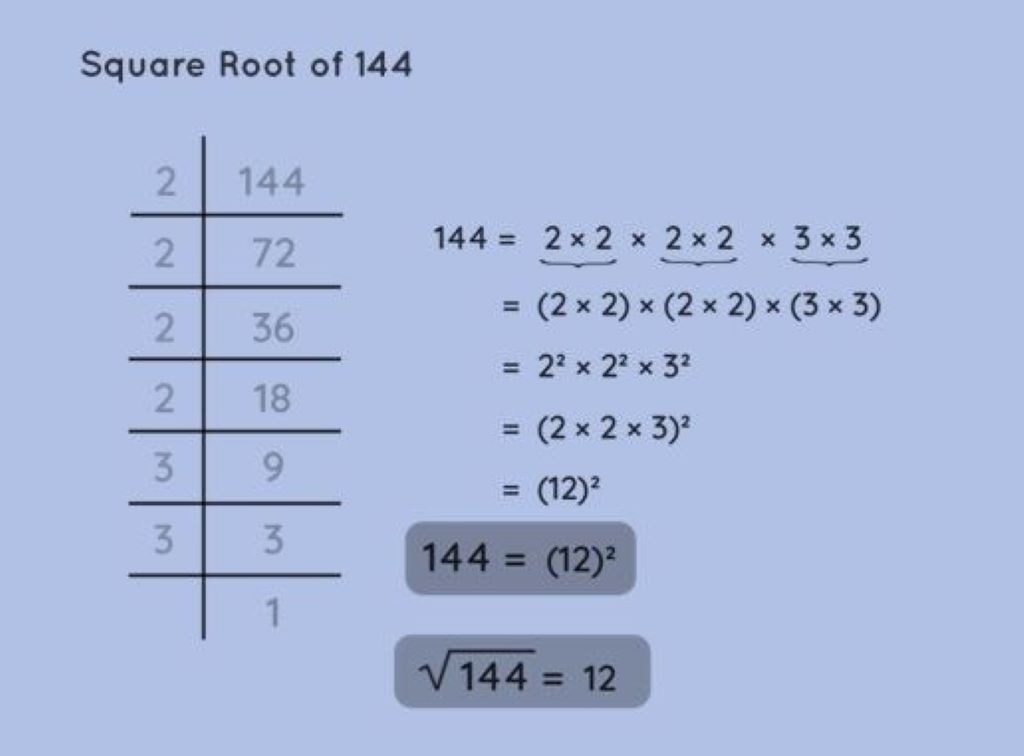
Understanding perfect squares up to 144 helps students recognize when square roots will be whole numbers. This pattern recognition supports both computation and problem-solving skills.
Comfort with decimal operations indicates readiness for working with irrational square roots. Students should understand that some square roots produce non-terminating, non-repeating decimals.
Building Confidence Through Practice
Regular practice with prerequisite skills builds student confidence for advanced topics. Spiral review ensures that foundational concepts remain fresh in student memory.
Connecting new learning to previous knowledge helps students see mathematical relationships. Understanding how square roots relate to exponents creates meaningful learning experiences.
Celebrating small victories in mathematical learning maintains student motivation. Recognizing progress in foundational skills encourages students to tackle more challenging concepts.
Supporting Struggling Learners
Some students need additional time to master prerequisite skills before moving to square roots. Identifying specific skill gaps helps teachers provide targeted intervention.
Multi-sensory approaches can help students who struggle with abstract mathematical concepts. Using manipulatives and visual aids makes learning more accessible.
Peer tutoring and collaborative learning provide additional support for students who need extra help. Working with classmates can reinforce learning and build confidence.
Preparing for Advanced Mathematics
Strong foundational skills in the areas discussed above prepare students for success with square roots and beyond. These concepts continue appearing in algebra, geometry, and higher mathematics courses.
Understanding the logical progression of mathematical topics helps students see the purpose behind their learning. Each skill builds toward more sophisticated mathematical thinking.
Conclusion
Success with square roots depends heavily on mastering foundational mathematical concepts first. Students need solid skills in basic operations, fractions, decimals, exponents, and geometric thinking before tackling square root problems effectively. The question of what grade is square root taught varies, but the prerequisite skills remain consistent across different curricula. By ensuring students have strong foundations in number sense, algebraic thinking, and problem-solving strategies, educators can set them up for success with this important mathematical concept. Regular assessment of these foundational skills helps teachers identify when students are ready to move forward with confidence.
Frequently Asked Questions
What mathematical skills should students master before learning square roots? Students should have strong multiplication and division skills, understand exponents and perfect squares, work confidently with fractions and decimals, and demonstrate solid number sense before approaching square root concepts.
How can parents help their children prepare for learning square roots? Parents can support their children by reinforcing multiplication tables, practicing fraction and decimal operations, and encouraging problem-solving through real-world applications like calculating areas and distances.
What are the warning signs that a student isn’t ready for square root instruction? Students who struggle with basic multiplication facts, have difficulty with fraction operations, or don’t understand exponent notation may need additional foundational work before learning square roots.
How do teachers typically introduce square root concepts? Most teachers begin with perfect squares and their corresponding square roots, then progress to estimating non-perfect square roots and using calculators for more complex calculations.
What role does geometry play in understanding square roots? Geometry provides concrete applications for square roots through area calculations, the Pythagorean theorem, and distance formulas, making abstract concepts more meaningful for students.
Read More:
Seven Popular Books That Explore the World of Casinos
What is Your Philosophy of Early Childhood Education? Exploring Ideas, Concepts, and Approaches



